Question

What is the length of segment DF?DF has a length of [Select]units. The trianglescan be proven similar by [Select]similarity

Answer 1

DF has a length of 36 units. The triangles can be proven similar by angle-angle similarity

Step-by-step explanation:

First we need to find the missing angles in each of the triangles to ascertain they have same angles:

From triangle ABC:

∠A + ∠B + ∠C = 180°

68 + 44 + ∠C = 180

112 + ∠C = 180

∠C = 180 -112 = 68°

from triangle DEF:

∠D + ∠E + ∠F = 180°

68 + ∠E + 44 = 180

∠E = 180 -(112) = 68°

The three angles in one triangle corresponds to the three angles of the second triangle

AB = 12, AC = 9

DE = 27, DF = ?

For two triangles to be similar, the ratio of the corresponding sides will be equal

∠A = ∠D, ∠B = ∠F, ∠C = ∠E

DE correponds to AC,

BC corresponds to EF

AB corresponds to DF

The ratio:

`\begin{gathered} (AC)/(DE)\text{ = }(BC)/(EF)\text{ = }(AB)/(DF) \\ (AC)/(DE)=\text{ }(AB)/(DF)\text{ (we use this due to the values we were given)} \\ (9)/(27)\text{ = }(12)/(DF) \end{gathered}`
`\begin{gathered} 9(DF)\text{ = 27(12)} \\ DF\text{ = }(27(12))/(9) \\ DF\text{ =3}6 \end{gathered}`

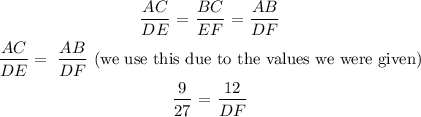
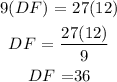
Since two angles in one triangle corresponds to two angles in the second triangle, it is similar by angle-angle similarity

DF has a length of 36 units. The triangles can be proven similar by angle-angle similarity