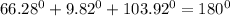Question

In the triangle below, suppose that mLL = (4x-9)º, m2M=(x-9)°, and m2N=rº.Find the degree measure of each angle in the triangle.(6x - 9)M0mL =Om 2M =N2m2N =(4x - 9)

Answer 1

Hello

assuming the triangle is the figure below

the sum total of all angles in a triangle is equal to 180 degree

`\begin{gathered} (4x-9)+(6x-9)+(x-9)=180\text{ } \\ \text{sum total of angles in a triangle is equal to 180 degree} \\ 4x-9+6x-9+x-9=180 \\ \text{collect like terms} \\ 11x-27=180 \\ 11x=180+27 \\ 11x=207 \\ x=(207)/(11) \\ x=18.82^0 \end{gathered}`

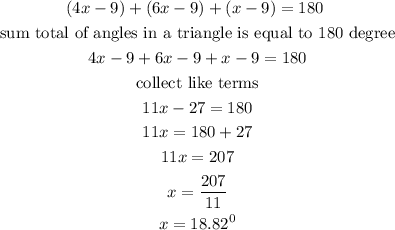
to find the degree measure in each angle, we can substitute x into the expression

`\begin{gathered} 4x-9 \\ x=18.82^0 \\ 4(18.82)-9=66.28^0 \end{gathered}`
`\begin{gathered} x-9 \\ \text{substitute x into the expression} \\ x=18.82^0 \\ 18.82-9=9.82^0 \end{gathered}`
`\begin{gathered} 6x-9 \\ x=18.82 \\ \text{substitute x into the expression} \\ 6(18.82)-9=103.92^0 \end{gathered}`

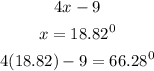
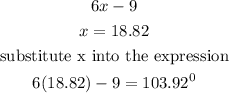
the degree measure of the angles are 66.28, 9.82 and 103.92 degrees respectively.

to prove the solution, the sum of the angles must be equal to 180 degree

`66.28^0+9.82^0+103.92^0=180^0`