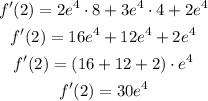f(x) = e^2x (x^3 + 1)
It can also be written as it follows:
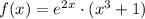
first we need to determine f'(x).
we can see this function as a product of two funcions:
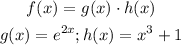
so, we can apply the Product rule
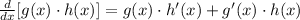
Let's determine the derivate of those two function
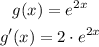
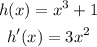
Now, we can use the functions g(x) and h(x) and its derivates to determine f'(x) using the Product rule
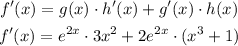
we can simplify this expression as it follows:
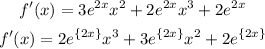
Finally, we need to replace x = 2 to find f'(2)
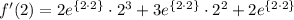
simplify: