Given:
Angle of elevation = 70 degrees.
Distance from her eyes to the ground = 1.66 meters
Horizontal distance from the base = 276 meters.
Let's find the height of the skyscraper.
Let's first sketch a figure which represents this situation:
To find the height of the skyscraper, apply the trigonometric ratio formula for tangent:
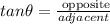
Where:
θ is the angle of elevation = 70 degrees
opposite side is the side opposite the angle = h
Adjacent side is the side adjacent the angle = 276 m
Thus, we have:
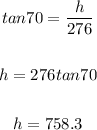
Now, the total height of the skyscraper will be:
758.3 + 1.66 = 759.96 ≈ 760 m
Therefore, the height of the skyscraper is 760 meters.
ANSWER: