a) The dot plot shows you how many kids scored a certain number of points during the Quiz.
I'll make a frequency table out of the graphic:
X | fi
11 | 1
12| 0
13| 1
14| 1
15| 1
16| 0
17| 2
18| 3
19| 3
20| 9
n= 21
The variable X: points scored by a student on a 20-point quiz
You can symbolize the students that scored higher than 16 poins as:
X>16
This expresion includes all students that scored 17, 18, 19 and 20 points
X>16 = (X=17)+(X=18)+(X=19)+(X=20)= 2+3+3+9= 17
17 Students scored more than 16 points in the quiz.
Divide it by 21 and multiply it by 100 to obtain the percentage:
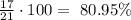
So, 80.95% of the students scored more than 16 points in the quiz.
b)
Regarding the shape of the distribution. They can be "symmetrical" or "asymmetrical"
Symmetrical distributions are normally centered around one value, for example the mean or median, and "move" equally to both sides of it.
Asymmetrical distribution usually show skeweness.
In this case if you see the dot plot, most of the values observed are on 20 points and then the rest flow to the left. To the right there are no values since the variable is defined between 0 and 20. This distribution is Asymmetrical and skewed to the left.
c)
An outlier is an observation that is significantly distant from the rest of the data set. They usually represent experimental errors (such as a measurement) or atypical observations. Some statistical measurements, such as the sample mean, are severely affected by this type of values and their presence tends to cause misleading results on a statistical analysis.
Values that are +/- 3 standard deviations from the center of the distribution can be considered to be outliers.
In this case, the one student that got 11 points at the quiz could be considered an outlier, since most of the distribution is at or near 20 points.