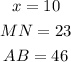Question

Show WhatGiven the fact that MN is the midsegment of triangle ABC, use the diagram below to write the equation for finding x.9x-44M MB2x+3NсEquation for finding x341 2

Answer 1

Since MN is the midsegment, then the proportion of the side is equal to 1/2. Thus the equation for finding x is the following equation.

`(2x+3)/(9x-44)=(1)/(2)`

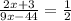
Thus, to solve for the value of x, multiply both sides of the equation by 2(9x-44). This will eliminate the denominators.

`2(2x+3)=9x-44`

Simplify both sides of the equation.

`4x+6=9x-44`

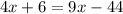
Isolate the variables on one side of the equation by subtracting 4x and adding 44 to both sides of the equation.

`\begin{gathered} 6+44=9x-4x \\ 50=5x \end{gathered}`

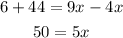
To obtain the value of x, divide both sides of the equation by 5.

`\begin{gathered} (50)/(5)=(5x)/(5) \\ 10=x \end{gathered}`

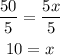
Thus, the value of x is 10.

To solve for MN, substitute the value of x, which is 10, into the expression 2x+3 and then simplify.

`\begin{gathered} MN=2(10)+3 \\ MN=20+3 \\ MN=23 \end{gathered}`

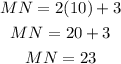
To solve for AB, substitute the value of x, which is 10, into the expression 9x-44 and then simplify.

`\begin{gathered} AB=9(10)-44 \\ AB=90-44 \\ AB=46 \end{gathered}`

Notice that AB is twice the measure of MN.

Therefore the answers in the blanks should be:

Equation: 2(2x+3)=9x-44

`\begin{gathered} x=10 \\ MN=23 \\ AB=46 \end{gathered}`