a) We have to find the parameters of the parabola (A, B and C) using three points as a system of linear equations.
With the points given we can write three equations:
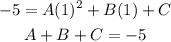
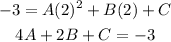
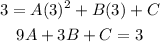
We will find the value of C from the first equation and then replace it in the second and third equation:
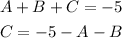
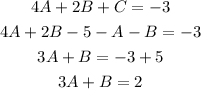

We now use the two new equations as a subsystem of equations to find A and B:

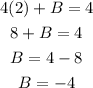
With the values of A and B, we can find C as:
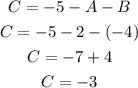
Then, the coefficients are A = 2, B = -4 and C = -3.
B) We can find the vertex of the parabola as:
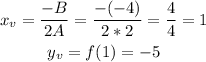
The vertex is already one of the values in the table.
The y-intercept is given by the value of C:
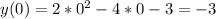
We can find the roots (or the x-intercepts) using the quadratic equation

The two interceps happen at approximately -0.581 and 2.581.
Knowing this points and the points from the table we can graph the parabola as:
C) In this case, we will have a minimum profit, as the parabola opens upward and has a minimum at its vertex.
This minimum is y = -5, which represents a negative profit of 5,000.
Answer:
A) A = 2, B = -4, C = -3
B) Graph
C) We have a minimum profit that is -$5,000