Question

The equation of line q is 5y - 4x = 10. Write the standard form of the equation of the line that fits the followingdescription:parallel to q and passes through the point at (-15, 8)

Answer 1

For 2 lines to be parallel, they have to have the same slope. It means we need to find the slope intercept point form of line q to find the slope of both lines.

`\begin{gathered} 5y-4x=10 \\ 5y=4x+10 \\ y=(4)/(5)x+2 \end{gathered}`

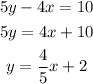
Both lines have a slope of 4/5.

Now, use the point slope formula to find the equation of the unknown line.

Remember the point slope formula:

`y-y1=m(x-x1)`

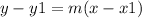
Where m is the slope and x1 and y1 are the coordinates of the given point (-15, 8). Replace these values in the formula:

`\begin{gathered} y-8=(4)/(5)(x+15) \\ y-8=(4)/(5)x+12 \\ y=(4)/(5)x+12+8 \\ y=(4)/(5)x+20 \end{gathered}`

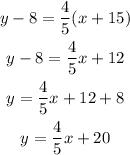
This is the slope intercept form of the equation of the unknown line. To convert it to standard form clear the constant term:

`\begin{gathered} y=(4)/(5)x+20 \\ 5y=4x+100 \\ 5y-4x=100 \end{gathered}`

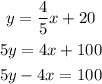
That is the equation in standard form of the line parallel to line q that passes through the point at (-15,8).