Exercise 1
Step-by-step explanation
We see that the graph is the plot of a polynomial function.
This polynomial has the following properties:
- Zeros:
• x₁ = -1 with multiplicity m₁ = 2, because the curve bounces the x-axis,
,
• x₂ = 2 with multiplicity m₂ = 1, because the curve crosses the x-axis,
,
• x₃ = 5 with multiplicity m₃ = 1, because the curve crosses the x-axis.
- y-intercept:
• y₀ = -4.
(a) The general form of this polynomial is:
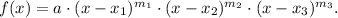
Where:
• x₁, x₂ and x₃ are zeros of the polynomial,
,
• m₁, m₂ and m₃ are the multiplicities,
,
• a is a constant factor.
Replacing the values from above, we get:

(b) Replacing the data of the y-intercept point (x, y) = (0, -4), we have:
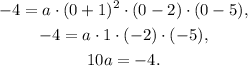
Solving for a, we get:
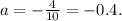
Replacing the value a = -0.4 in the equation of the polynomial, we get:
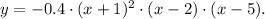
Answer
(a) The factored form of the graph is:
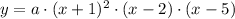
(b) The value of the constant a is:

The complete equation of the curve is:
