Let l be the length of the rectangle, then we can set the following equation:
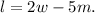
Where w is the width of the rectangle. Now, the formula for the area of a rectangle is:
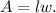
Solving the above equation for l, we get:
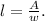
Substituting l=A/w in the first equation we get:
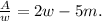
Solving for w, and considering that A=52 m²we get:
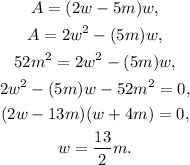
Substituting w=4m in the first equation we get:

Answer:
Length: 8 m,
Width: 6.5 m.