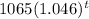Question

retry this question belowA population numbers 1,065 organisms initially and increases by 4.6% each year.Suppose Prepresents population, and t the number of years of growth. Write an exponentialmodel to represent this situation.P=

Answer 1

Given: a population numbers 1065 organism initially and incresed by 4.6% each year

Find: the exonential model to represents the situation.

Step-by-step explanation: the exponential model fit the same pattern

`P=a(b)^t`

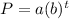
where a is initial amount , b is amount of either grow or sink .

so

`a=1065`

and

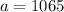
`\begin{gathered} b=1+0.046 \\ b=1.046 \end{gathered}`

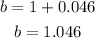
so the exponentail model become

`1065(1.046)^t`

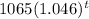
Final answer: The required exponential model to represent the situation is

`1065(1.046)^t`