Question

You order a glass of lemonade, 150 mL, in a restaurant only to discover that it is warm and too sweet. The sugar concentration of the lemonade is 2.27 M but you would like it to be reduced to a concentration of 1.88 M.How many grams of ice should you add to the lemonade, knowing that only a third of the ice will melt before you take your first sip? (Assume the density of water is 1.00 g/mL)

Answer 1

Since no sugar will be added or removed, the number or moles of it in the glas won't change.

Let's call this quantity:

`n_s`

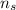
The molar concetrnation can be written as the followin equation:

`C=(n_s)/(V)`

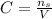
Where C is the concentration given the number of moles of sugar and the volume V.

We can rewrite this as:

`n_s=C\cdot V`

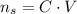
Now, before the ice melts, the volume of the lemonate is 150 mL and the sugar concentration is 2.27 mol/L. Let's call this situation 1:

`n_s=C_1\cdot V_1`

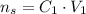
After the ice melt the one third it will, we will have a certain volume and the concentration we want 1.88 mol/L. Let's call this situation 2:

`n_s=C_2\cdot V_2`

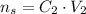
Now, we can put thouse tofether:

`\begin{gathered} n_s=n_s \\ C_1\cdot V_1=C_2\cdot V_2 \end{gathered}`

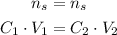
And we can solve for the unknown volume of situation 2:

`V_2=(C_1\cdot V_1)/(C_2)=(2.27M\cdot150mL)/(1.88M)=(340.5)/(1.88)mL=181.117\ldots mL\approx181mL`

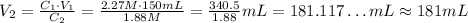
Since the final volume is approximately 181 mL, the difference between it and the initial volume is the volume of water that came from the melted part of the ice:

`181mL-150mL=31mL`

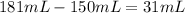
Since we assume that the density of the water is 1.00 g/mL, we can calculate the mass it represents:

`\begin{gathered} \rho=(m)/(V)_{} \\ m=\rho\cdot V=1.00g/mL\cdot31mL=31g \end{gathered}`

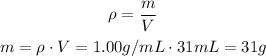
And since this is only 1 third of the ice (the rest won;t melt), we know that the whole ice will have three times this mass:

`m_(ice)=3\cdot31g=93g`

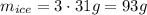
So, it should be added approximatelt 93 grams of ice.