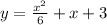Question

What is the standard equation for a parabola with focus (-3,3) and directrix y=0?

Answer 1

Answer:

The standard equation of the parabola is:

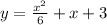
`y=(x^2)/(6)+x+3`Step-by-step explanation:

The focus of the parabola, (h, f) = (-3, 3)

The directrix: y = 0

The equation of a parabola is of the form:

`y=(1)/(4(f-k))(x-h)^2+k`

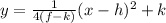
The distance from the focus to the vertex is equal to the distance from the vertex to the directrix

f - k = k - y

3 - k = k - 0

k + k = 3 + 0

2k = 3

k = 3/2

Substitute k = 3/2, f = 3, and h = -3 into the equation above

`\begin{gathered} y=(1)/(4(3-(3)/(2)))(x-(-3))^2+(3)/(2) \\ y=(1)/(4((3)/(2)))(x+3)^2+(3)/(2) \\ y=(1)/(6)(x+3)^2+(3)/(2) \\ y=((x+3)^2)/(6)+(3)/(2) \end{gathered}`

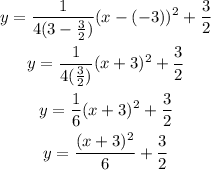
This can be further simplified as:

`\begin{gathered} y=(x^2+6x+9)/(6)+(3)/(2) \\ y=(x^2+6x+9+9)/(6) \\ y=(x^2+6x+18)/(6) \\ y=(x^2)/(6)+(6x)/(6)+(18)/(6) \\ y=(x^2)/(6)+x+3 \end{gathered}`

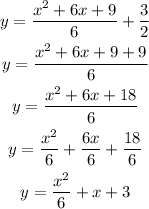
Therefore, the standard equation of the parabola is:

`y=(x^2)/(6)+x+3`