We are given the following problem:
To determine the electric force between the protons we will use Coulomb's law, that is:
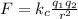
Where "k" is Coulomb's constant and is equivalent to:
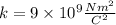
Since the charges are equal we have:
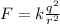
Replacing the values:
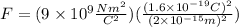
Simplifying:
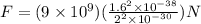
Solving the operations:
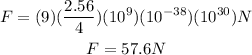
Therefore, the magnitude of the repulsive force is 57.6N.