Question

X²+10x-3=0 Square process

Answer 1

start by adding 3 on both sides of the equation

`\begin{gathered} x^2+10x-3+3=0+3^{} \\ x^2+10x=3\text{ equation (1)} \end{gathered}`

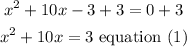
in order for the expression to become a perfect square we must remember

`(x+a)^2=x^2+2\cdot a\cdot x+a^(22)`

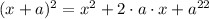
using the term 10x we can find the term a in the expression above to complete the square

`\begin{gathered} 10x=2\cdot a\cdot x \\ (10x)/(2x)=a \\ a=5 \end{gathered}`

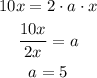
in order to complete the square must add a square on both sides

`\begin{gathered} (x+5)^2=x^2+2\cdot5\cdot x+(5)^2 \\ (x+5)^2=x^2+10x+25 \end{gathered}`

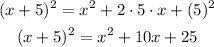
add 25 on both sides of equation 1

`\begin{gathered} x^2+10x+25=3+25 \\ x^2+10x+25=28 \end{gathered}`

write the expression to the left as a perfect square

`(x+5)^2=28`

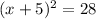
take the square root on both sides

`\begin{gathered} \sqrt[]{(x+5)^2}=\sqrt[]{28} \\ x+5=\pm\sqrt[]{28} \end{gathered}`

to find the solutions substract 5 on both sides for both the solutions

`\begin{gathered} x+5-5=-5\pm\sqrt[]{28} \\ x_1=-5+\sqrt[]{28}=-5+2\cdot\sqrt[]{7} \\ x_2=-5-\sqrt[]{28}=-5-2\cdot\sqrt[]{7} \end{gathered}`