Question

Find the vertex and write the quadratic function in vertex form (which our OpenStax textbook also callsthe standard form).f(x) = 22 – 8x + 80Give the vertex. Enter your answer as a point (a,b).Vertex:Enter the coordinates of the vertex to write f(x) in vertex form:f(x) = (2- Number )2 + NumberWhich of the following best represents the graph of this function, considering the location (quadrant) of

Answer 1

A parabola equation written in vertex form is given by

`f(x)=a(x-h)^2+k`

where (h, k) represents the coordinates of the vertex. Our equation is

`f(x)=x^2-8x+80`

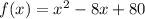
To rewrite this function in vertex form, we need to use the complete the square method. When we expand the binomial of a difference, we have

`(x-a)^2=x^2-2ax+a^2`

If we compare the expanded form with our function, we have the following correspondence

`-8=-2a\implies a=4`

Then, we can rewrite our expression as

`\begin{gathered} f(x)=x^2-8x+80 \\ =x^2-8x+16+64 \\ =(x)^2-2(4)(x)+(4)^2+64 \\ =(x-4)^2+64 \end{gathered}`

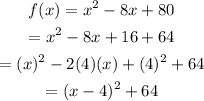
Comparing this equation to the vertex form, the vertex of our parabola is

`(4,64)`

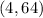
And the equation is

`f(x)=(x-4)^2+64`

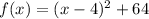
The graph of this parabola is