Given:
Distance travelled with the wind = 260 miles
Distance travelled against the wind = 180 miles
Speed of wind = 20 mph.
Let's find the rate of the plane in still air.
Apply the formula:
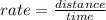
Thus, we have the equations:
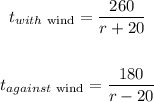
Now, the rate in still air will be:
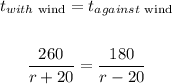
Now, let's solve for r in the equation above.
Cross multiply:
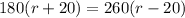
Divide both sides of the equation by 20:

Solving further:
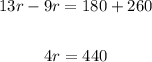
Divide both sides by 4:
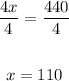
Therefore, the rate in still air is 110 mph.
ANSWER:
110 mph