1 Answer

Ask a Question

NKandel · Answer 1 · 2023-07-13T23:37:28+0000

(i) The bearing of B from A and angle x are supplementary, then:

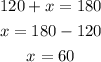
$\begin{gathered} 120\degree+x=180\degree \\ x=180\degree-120\degree \\ x=60\degree \end{gathered}$

(ii)

From the above diagram, the bearing angle of A from B is:

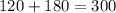
$120\degree+180\degree=300\degree$

(iii)

From the above diagram, the bearing angle of C from B is:

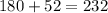
$180\degree+52\degree=232\degree$

(iv)

Applying the law of cosines with the sides AB = 145m and CB = 240 m, and the angle ABC = 68°, the distance AC is:

$\begin{gathered} AC^2=AB^2+CB^2-2\cdot AB\cdot CB\cdot cos\left(\angle ABC\right) \\ AC^2=145^2+240^2-2\cdot145\cdot240\cdot cos(68\degree) \\ AC^2=21025+57600-69600\cdot cos(68\operatorname{\degree}) \\ AC^2=52552.3811 \\ AC=√(52552.3811) \\ AC\approx229\text{ m} \end{gathered}$

2. Let A, B and c be three towers. The bearing of B from A is 120° and angle BC is-example-1

2. Let A, B and c be three towers. The bearing of B from A is 120° and angle BC is-example-2

2. Let A, B and c be three towers. The bearing of B from A is 120° and angle BC is-example-3

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions