Solution
Given the following scores below
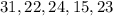
To find the sum of squares of the deviations,
Firstly, we find the mean, the formula to find the mean of ungrouped data is
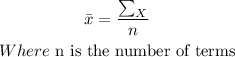
Where n = 5
Substitute the given data into the formula to find the mean of ungrouped data
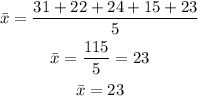
Secondly, we subtract the mean from each of the values given as shown below
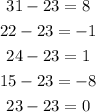
Then, to find the sum of squares of the deviations
We add the square of each of the deviations deduced above
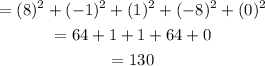
Hence, the sum of squares is 130