We will determine the surface area of the solid as follows:
*First: We can see that the solid is composed of three pairs of sides, so we will have to calculate the area of just 3 different faces.
*Second: We determine the areas:
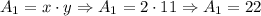
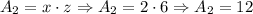
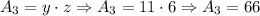
*Third: We add the areas to determine the surface area:
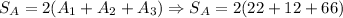
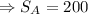
So, the surface area is 200 square units. [Option C