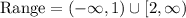To answer this question, we can see a piecewise function:
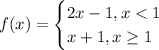
They are two different lines in the slope-intercept form.
We will consider the given steps to graph the function.
Values for the 2x - 1 function
We can see that this function will be for values of x less than 1 (not equal to 1), x<1. Then, we need to find, at least, two pairs of values to sketch the graph in this part. Then, we have:


And we need to know the value at the right extreme of this function, a value for which the function is not defined, x = 1:

We need to be careful here since the function is NOT defined for x = 1. We are finding a limit value.
Then, the values to graph here are: (-2, -5), (-1, -3), and the value not defined for this function (1, 1) . Or in a table:
x y
-2 -5
-1 -3
1 1 (not defined for this point, only for purpose of graphing).
Values for the x + 1 function
We can proceed similarly as before to find the other values. In this case, the function is, indeed, defined for x = 1. So we can proceed as follows:

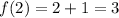

Now, we have the next values to graph this function: (1, 2), (2, 3), (3, 4). We can construct a table for this:
x y
1 2
2 3
3 4
The graph is (considering all the work done):
We can see that the function is not defined for the red line, y = 2x - 1, but it does for the blue line, y = x + 1. We can graph the function with no coordinates as follows:
We can see on the graph the solid blue point indicating that the function is defined for x = 1, y = 2 for the function, x + 1, while is it not defined for x = 1 for the function y = x + 1.
The domain and range for this piecewise function are:
• Domain ---> (-∞, ∞). Since we have the function is defined for x<1 (-∞, 1) and x≧1, that is, [1, ∞).
,
• Range ---> the piecewise has a range (-∞, 1) U [2, ∞). We can see that the values between y = 1 and y <2 are not part of the range. If we write this in interval notation we have (1, 2).
In summary, we have:
The function can be graphed as follows (notice the solid blue point indicating that, for x = 1, the value of the function is 2):
The domain of this piecewise function is (in interval notation):
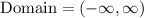
The range of the function is (in interval notation):