Question

Which equation should be used to calculate the 43rd partial sum for the arithmetic sequence (an)=(3/8n+1/2)

Answer 1

The arithmetic sequence is given

`a_n=(3)/(8)n+(1)/(2)`

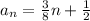
To determine the 43rd partial sum of the arithmetic sequence ,use the sum formula.

`S_n=(n)/(2)(a_1+a_n)`

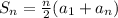
First determine the first term ,

`a_1=(3)/(8)*1+(1)/(2)=(3)/(8)+(1)/(2)=(7)/(8)`

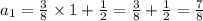
To determine the last term that is

`a_(43)=(3)/(8)*43+(1)/(2)=(129+4)/(8)=(133)/(8)`

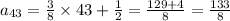
Substitute the value of last term and first term in the sum formula

`S_(43)=(43)/(2)((7)/(8)+(133)/(8))`

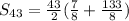
Hence the correct option is B.