Question

Find sin 0 and tan 0 when cos 0 = 2/5

Answer 1

`\begin{gathered} \sin \theta=\frac{\sqrt[]{21}}{5} \\ \tan \theta=\frac{\sqrt[]{21}}{2} \end{gathered}`

Explanation:

We have the following:

`\cos \theta=(2)/(5)`

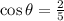
Which means that the adjacent leg of the triangle is equal to 2 and the hypotenuse is equal to 5.

We can calculate the value of the opposite leg by means of the Pythagorean theorem as follows

`\begin{gathered} h^2=a^2+b^2 \\ 5^2=2^2+b^2 \\ \text{solving for b:} \\ b^2=25-4 \\ b=\sqrt[]{21} \end{gathered}`

Knowing the value of the opposite leg we can calculate the value of the other trigonometric ratios:

`\begin{gathered} \sin \theta=\frac{\text{opposite}}{\text{hypotenuse}}=\frac{\sqrt[]{21}}{5} \\ \tan \theta=\frac{\text{opposite}}{\text{adjacent}}=\frac{\sqrt[]{21}}{2} \end{gathered}`