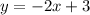Question

Find the slope, y-intercept and equation of the line for the points (0,3) (2,-1) show work please

Answer 1

we are asked to determine the slope of the line that passes through the points (0, 3) and (2, -1). To do that we need to use the formula for the slope of a line:

`m=(y_2-y_1)/(x_2-x_1)`

Where:

`\begin{gathered} (x_1,y_1)=(0,3) \\ (x_2,y_2)=(2,-1) \end{gathered}`

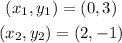
Replacing in the formula:

`m=(-1-3)/(2-0)`

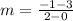
Solving the operations:

`m=-(4)/(2)=-2`

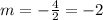
therefore, the slope is -2.

To determine the y-intercept we can use the point (0,3), since this means that when x = 0, y = 3. Since the y-intercept is the value of "y" when x = 0, this means that the y-intercept is 3.

To determine the equation of the line we need to use the general form of a line equation:

`y=mx+b`

Where "m" is the slope and "b" the y-intercept. Replacing the value of the slope and "b"

`y=-2x+3`