Question

A train locomotive pulls a train with a mass of 1.30 ✕ 107 kg on level rails. The locomotive exerts a constant force of 6.60 ✕ 105 N on the train. How much time does it take to increase the speed of the train from rest to 74.0 km/h? (Ignore any resistance force from the rails on the wheels of the train. Enter your answer in minutes.)_____ min

Answer 1

According to Newton's Second Law of Motion, the acceleration a of an object with mass m that experiences a net force F is:

`a=(F)/(m)`

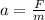
Replace F=6.60*10^5N and m=1.30*10^7kg to find the acceleration of the train:

`a=(6.60*10^5N)/(1.30*10^7kg)=5.077*10^(-2)(m)/(s^2)`

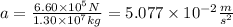
The time t that it takes for an object with acceleration a to reach a speed v starting from rest is:

`t=(v)/(a)`

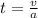
Replace v=74.0km/h, a=5.077*10^-2m/s^2 and convert the speed to m/s to find the time that it takes for the train to reach that speed. Convert the final answer to minutes:

`t=(74.0(km)/(h)*(1(m)/(s))/(3.6(km)/(h)))/(5.077*10^(-2)(m)/(s^2))=404.88...s=6.748...min\approx6.75min`

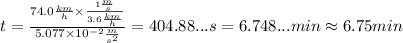
Therefore, the time that it takes for the train to reach a speed of 74.0km/h is approximately 6.75 min.