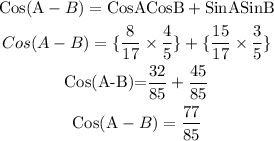Question

For positive acute angles A and B, it is known that cos A = 8/17 and sin B = 3/5. Find the value of sin(A - B) in simplest form.

Answer 1

The expansion of Cos(A-B) is:

`\text{Cos(A}-B)=CosACosB+SinASinB`

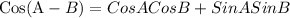
We are provided with the following:

`\text{Cos A=}(8)/(17),Sin\text{ B=}(3)/(5)`

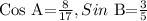
We will have to obtain the values of Cos B and Sin A. Thus, we have:

To be obtain Sin A, we have to get the value of the third side, which is the opposite side, by applying the pythagoras theorem. Thus, we have:

`\begin{gathered} (\text{Hypotenuse)}^2=(\text{Opposite)}^2+(\text{Adjacent)}^2 \\ 17^2=O^2+8^2 \\ 289=O^2+64 \\ 289-64=O^2 \\ O^2=225 \\ O=\sqrt[]{225} \\ O=15 \\ \text{Thus, Sin A=}\frac{Opposite}{\text{Hypotenuse}} \\ Sin\text{ A=}(15)/(17) \end{gathered}`

To be obtain Cos B, we have to get the value of the third side, which is the adjacent side, by applying the pythagoras theorem. Thus, we have:

`\begin{gathered} \text{Hyp}^2=\text{Opp}^2+\text{Adj}^2 \\ 5^2=3^2+A^2 \\ 25=9+A^2 \\ 25-9=A^2 \\ A^2=16 \\ A=\sqrt[]{16} \\ A=4 \\ \text{Thus Cos B=}\frac{Adjacent\text{ }}{\text{Hypotensue}} \\ \text{Cos B=}(4)/(5) \end{gathered}`

Now that we have obtained the values of Cos B and Sin A, we can then go on to solve the original problem.

`\begin{gathered} \text{Cos(A}-B)=\text{CosACosB}+\text{SinASinB} \\ Cos(A-B)=\mleft\lbrace(8)/(17)*(4)/(5)\mright\rbrace+\mleft\lbrace(15)/(17)*(3)/(5)\mright\rbrace \\ \text{Cos(A-B)=}(32)/(85)+(45)/(85)_{} \\ \text{Cos(A}-B)=(77)/(85) \end{gathered}`