Given that the average student loan debt is $25,900.
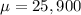
The standard deviation is $10,200.
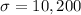
Let X be the student loan debt of a randomly selected college graduate.
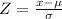
When x =$14,950, we have;

When x=$28,050, we have;
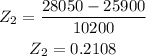
Then,
[tex]\begin{gathered} P(-1.0735
The probability that the college graduate has between $14,950 and $28,050 in student loan debt is 0.4420