Answer:
4.737 N/m
Step-by-step explanation:
The period of a mass-spring system is calculated as
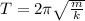
Where m is the mass and k is the spring constant. Solving for k, we get
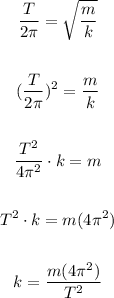
Then, replacing m = 750 g = 0.75 kg and T = 2.5s, we get:
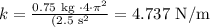
Therefore, the spring constant must be 4.737 N/m