Given:
Total numbers = 9, 8, 7, 5, 3, 1 ==> 6 numbers
Let's find the number of positive three digit integers whose digits are among the given numbers in which none of the digits are the same.
Here, we are to use permutation since the ordering of the numbers is important.
Apply the formula:
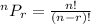
Where:
n = 6
r = 3
We have:
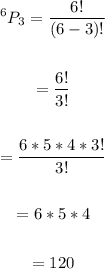
Therefore, the number of 3 digit integers is 120.
ANSWER:
120