Given data
*The given radius of a spherical container is r_1 = 14.5 cm
*The given temperature of the gas is T_1 = 179 K
*The given pressure is P_1 = 1.97 atm
*The given another pressure is P_2 = 3.73 atm
*The given another temperature is T_2 = 293 K
(A)
The radius (in cm) of the container is calculated by using the relation as
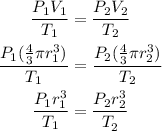
Substitute the known values in the above expression as
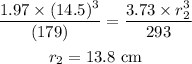
Hence, the radius of the container is r_2 = 13.8 cm