Question

A cat and his frictionless roller-skates have a total mass of 2kg. It was rolling at 5m/s to the right, and then crashed into a 3 kg cake that had ben left on the floor. The cake was initially at rest, and the cat gets stuck inside it.How does the total kinetic energy of the cat-cake system change during this collision, and what is their speed immediately afterword?Question 3 options:Kinetic EnergySpeedIncreases2 m/sKinetic EnergySpeedIncreases3.2 m/sKinetic EnergySpeedIncreases2.5 m/sKinetic EnergySpeedDecreases2.5 m/sKinetic EnergySpeedDecreases2 m/sKinetic EnergySpeedDecreases3.2 m/s

Answer 1

Given data:

The mass of cat with skate is m=2 kg.

The speed of cat with skate is u=5 m/s.

The mass of the cake is M=3 kg.

Applying the conservation of momentum to calculate the velocity,

`mu=(m+M)V`

Here, V is the combined velocity of cat and cake.

Substitute the values in above equation,

`\begin{gathered} (2)(5)=(2+3)V \\ V=2\text{ m/s} \end{gathered}`

Thus, the final velocity immediately afterword is 2 m/s.

The initial kinetic energy will be,

`\begin{gathered} KE_i=(1)/(2)mu^2 \\ KE_i=(1)/(2)(2)(5)^2 \\ KE_i=25\text{ J} \end{gathered}`

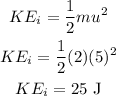
The final kinetic energy will be,

`\begin{gathered} KE_f=(1)/(2)(m+M)V^2 \\ KE_f=(1)/(2)(2+3)(2)^2 \\ KE_f=10\text{ J} \end{gathered}`

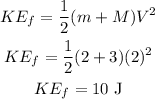
As calculated above, the final kinetic energy is less than the initial kinetic energy.

Thus, the final kinetic energy will be decreased.

Thus, option 5 is correct.