Question

AÉ is an angle bisector of ZBAC.If mZBAE = x + 30 and mZEAC = 3x - 10,determine mZEAC.BEСmZEAC = [ ? 1°Enter

Answer 1

We are given the following triangle

We want to find the measure of angle EAC. Note that this measure is 3x-10, so we need to find the value of x to find the measure of the angle. To do so, we will start by using the fact that line AE bisects the angle BAC. This means that line AE splits the angle BAC into two angles (BAE and EAC) that have the same measure. Since angle BAE has a measure of x+30, we end up having the following equation

`x+30=3x-10`

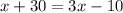
now, we want to solve this equation for x. So we start by adding 10 on both sides. Then, we get

`x+30+10=3x`

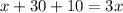
which is equivalent to

`x+40=3x`

now, we subtract x on both sides, so we get

`40=3x-x=2x`

Finally, we divide both sides by 2. Then we get

`x=(40)/(2)=20`

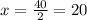
Since the measure of angle EAC is 3x-10, we replace this value to find the measure of the angle. So we have that

`\text{EAC}=3x-10=3\cdot20-10=60-10=50`

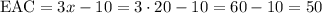
Then, the measure of angle EAC is 50°