Answer:
a) y = -0.131x + 50.1
b) The predicted age of the best actor is within 5 years of the actual best actor's age
Step-by-step explanation:
We were given a dataset. We will use this dataset to plot the graph as shown below:
We will plot the age of the best actor vs that of the best actress to obtain the graph below:
The equation of the straight line is given by:

The equation is: y = -0.131x + 50.1
When the best actress age is 59, the predicted age of the best actor is obtained as shown below
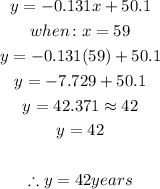
At 42 years, the predicted age is 4 years lesser than the actual best actor's age
Hence, the predicted age of the best actor is within 5 years of the actual best actor's age