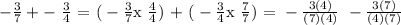Question

-3/7 + -3/4 what is the answer

Answer 1

Problem:

solve -3/7 + -3/4

Solution:

Consider

`-(3)/(7)+-\text{ }(3)/(4)`

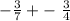
our goal is to have the same denominator so we do the following trick:

`-(3)/(7)+-\text{ }(3)/(4)\text{ = (}-(3)/(7)\text{x }(4)/(4))\text{ + (}-(3)/(4)\text{x }(7)/(7))`

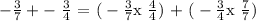
Notice that we multiply the numerator and denominator of one fraction by a fraction that contains the denominator of the other fraction in the equation. Now, the above equation is equivalent to:

`-(3)/(7)+-\text{ }(3)/(4)\text{ = (}-(3)/(7)\text{x }(4)/(4))\text{ + (}-(3)/(4)\text{x }(7)/(7))\text{ = }-(3(4))/((7)(4))\text{ }-(3(7))/((4)(7))`

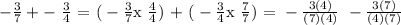
that is:

`-(3)/(7)+-\text{ }(3)/(4)\text{ = (}-(3)/(7)\text{x }(4)/(4))\text{ + (}-(3)/(4)\text{x }(7)/(7))\text{ = }-(3(4))/((7)(4))\text{ }-(3(7))/((4)(7))`