Given:
Principal, P = $4000
Interest rate, r = 3% = 0.03
Time, t = 15 years.
Number of times comounded, n = monthly = 12 months a year
Let's find the final Amount in the account after 15 years.
Apply the compound interest formula

Where:
A is the final amount.
P = $4000
r = 0.03
t = 15
n = 12
Thus, we have:

Solving further:
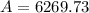
Therefore, the amount in the account in 15 years will be $6269.73
ANSWER:
$6269.73