Question

What is the probability that a randomly chosen day is one when he drank exactly of coffee and is one when he slept exactly 8 hours?

Answer 1

Probability is defined as,

`\text{Probability}=\frac{required\text{ outcome}}{possible\text{ outcome}}`

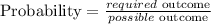
Let the prob that a day is one he drank exactly 0 cups of coffee be P(A)

Let the probability that a day is when he slept 8 hours be P(B)

Let the probabilty that a day is one he drank exactly 0 cups of coffee or slept for 8 hours be P(C)

`\begin{gathered} P(A)=0.2 \\ P(B)=0.3 \\ P(C)=0.4 \end{gathered}`

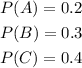
Probability he drank 0 cups of coffee and slept for 8 hours is an independent event hence, can be represented below as,

`P(A\text{ OR B) = P(A) }* P(B)`

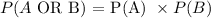
Substituting the variables P(A) and P(B) into the given formula above,

`P(A\text{ OR B) = 0.2 }*\text{ 0.3 = 0.06}`

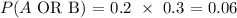
Hence, the prob is 0.06.