Question

Assume that the stopping distance of van varies directly with the square of the speed. A Van travelling 40 miles per hour can stop in 80'. If Van travelling 64 miles per hour, What is it stopping distance?

Answer 1

We have a proportional relationship between the stopping distance d and the square of the speed v^2. This can be written as:

`d=k\cdot v^2`

where k is a constant we have to find.

We can calculate k knowing that, if the speed is v = 40 miles per hour, the distance is 80 feet. Then:

`\begin{gathered} d=k\cdot v^2\longrightarrow k=(d)/(v^2) \\ k=(d)/(v^2)=(80)/(40^2)=(80)/(1600)=0.05 \end{gathered}`

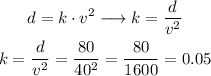
NOTE: This value of k correspond to the relation when d is expressed in feet and v in miles per hour.

Now, we can calculate the stopping distance for v = 64 miles per hour:

`\begin{gathered} d=k\cdot v^2 \\ d=0.05\cdot64^2=0.05\cdot4096=204.8\text{ ft} \end{gathered}`

Answer: 204.8 feet.