In the given right angled trianged, the hypotenuse side is 6 and the adjacent side is x.
The angle formed by the hypotenuse and the adjacent side is 60 degree
The objective is to find the value of the adjacent side x.
SInce, we are provided with hypotenuse and adjacent, use cosine formula.
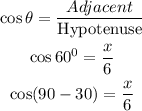
It is known that
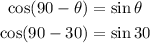
So,
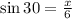
From the trignometric table the value of sin 30 is 1/2. Substitute the value in the above equation.
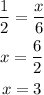
Hence, the length of the hypotenuse side x is 3.