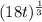How do I write 3√18t using rational exponents?

Question

asked May 22, 2023 203k views

1 Answer

Dtgee · Answer 1 · 2023-05-28T15:41:48+0000

DEFINITIONS:

Rational Exponents are also called Fractional Exponents. Consider the expression below:

$a^{(m)/(n)}$

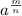
The fractional exponent m/n indicates a radical with index n and exponent m, such that

$a^{(m)/(n)}=\sqrt[n]{a^m}$

SOLUTION TO THE QUESTION:

The question is given to be:

$\sqrt[3]{18t}$

Applying the rule of exponents we have stated earlier, we can write out the expression to be:

where, in our case

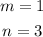
$\begin{gathered} m=1 \\ n=3 \end{gathered}$

$\sqrt[3]{18t}=(18t)^{(1)/(3)}$

Therefore, the answer is:

$(18t)^{(1)/(3)}$