Question

A roulette wheel has 36 slots around the rim; 34 slots are numbered 1-34. Half of these slots are red, and the other half are black. The remaining 2 slots are numbered 0 and 00 and are green. As the roulette wheel is spun in one direction, a small ivory ball is rolled along the rim in the opposite direction. The ball has an equality chance of falling on one of the 36 slots. Find the probabilities of parts (A) thru (D) below. a. Ball lands in a black slot.

Answer 1

Let us write the formula for probability,

`\text{Probability}=\frac{Number\text{ of favourable outcomes}}{\text{Total number of outcomes}}`

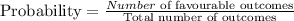
The number of balls that lands in the black slot are 17, because we were told that half of the slots are red and half of the slots are black.

`\begin{gathered} \text{The number of balls that lands in black slot=}(34)/(2) \\ =17 \end{gathered}`

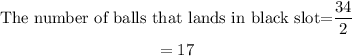
The total number of slots= 36

The probability of balls that land in a black slot will be,

`\begin{gathered} P(\text{ball lands in a black slot)=}\frac{The\text{ number of balls in the black slot}}{\text{Total slots}} \\ =(17)/(36)=(17)/(36) \end{gathered}`

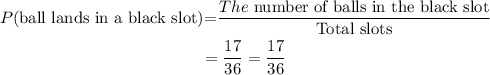
Hence, P(ball lands in a black slot)= 17/36.