Question

What is x in the equation??

Answer 1

`4x^2-27x+18`

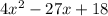
We have the above equation, this is a quadratic polynomial, which is a polynomial with two real roots (two x-axis crossings), therefore x has two possible solutions.

Now, let's factor this equation and find the values for x.

`\begin{gathered} (4x^2-3x)+(-24x+18) \\ x(4x-3)+6(4x-3) \end{gathered}`

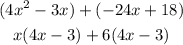
Now, we factor in the common term 4x-3.

`(4x-3)(x-6)`

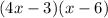
Now, let's solve for the two values of x

`\begin{gathered} x-6=0 \\ x=6 \end{gathered}`
`\begin{gathered} 4x-3=0 \\ 4x=3 \\ x=(3)/(4)=0.75 \end{gathered}`

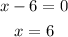
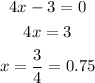
In conclusion, x can take the value of x = 6 or x = 0.75

In the following graph we can see this: