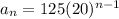Question

The numbers of points that a player must accumulate to reach the next level of a video game form ageometric sequence where an is the number of points needed to complete level n. You need 50,000points to complete level 3 and 20,000,000 points to compete level 5.The explicit rule for the geometric sequence is

Answer 1

So,

Here we can identify the following terms of the given sequence:

`\begin{gathered} a_3=50,000 \\ a_5=20,000,000 \end{gathered}`

What we're going to do to find an explicit rule for this geometric sequence is to replace each term in the general form:

`a_n=a_1(r)^(n-1)`

We're given that:

`\begin{gathered} a_3=50,000 \\ a_5=20,000,000 \end{gathered}`

So, replacing we got:

`\begin{gathered} 50,000=a_1(r)^(3-1)\to50,000=a_1(r)^2 \\ 20,000,000=a_1(r)^(5-1)_{}\to20,000,000=a_1(r)^4_{} \end{gathered}`

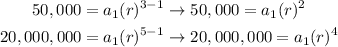
As you can see, here we have the following system:

`\begin{cases}50,000=a_1(r)^2 \\ 20,000,000=a_1(r)^4_{}\end{cases}`

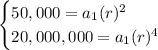
We could divide equation 2 by equation 1 to find the value of r:

`\frac{20,000,000=a_1(r)^4_{}}{50,000=a_1(r)^2}\to400=(r)^2\to r=20`

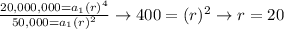
Now that we know that r=20, we could find the value of a1:

`\begin{gathered} 50,000=a_1(20)^2 \\ 50,000=a_1(400) \\ a_1=(50,000)/(400)=125 \end{gathered}`

Therefore, the explicit rule will be:

`a_n=125(20)^(n-1)`