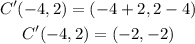We are given a triangle and we are asked to translate its vertices two units to the right and four units down. To do that we will use the following rule for the transformation:
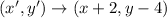
The coordinates of vertex A is:
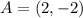
Applying the rule we get:
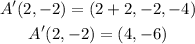
The coordinates of point B are:
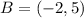
Applying the rule we get:
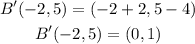
The coordinates of point C:
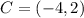
Applying the rule: