Step-by-step explanation:
Adults distracted by their smartphones = 50%
To get probability of exacty 4 adults getting distracted, we would apply binomial distribution
p = 50% = 0.5
Probability of exacty 4 adults getting distarcted = P(x = 4)

Inserting the values:
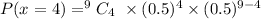
![undefined]()