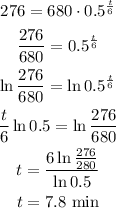Question

Element X decays radioactively with a half life of 6 minutes. If there are 680 grams ofElement X, how long, to the nearest tenth of a minute, would it take the element todecay to 276 grams?

Answer 1

Given

half life in 6m

Initial 680g

Procedure

`y=a(0.5)^{(t)/(h)}`

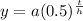
This is the model we can use to calculate the decay. But we must recognize the values of a and of h

The value of a corresponds to the initial value of the population, which in our case is 680g.

While the value of h will be the number of minutes it takes to reach its half-life. Therefore:

`y=680\cdot0.5^{(t)/(6)}`

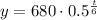
With this formula, we can now proceed:

`\begin{gathered} 276=680\cdot0.5^{(t)/(6)} \\ (276)/(680)=0.5^{(t)/(6)} \\ \ln (276)/(680)=\ln 0.5^{(t)/(6)}^{} \\ (t)/(6)\ln 0.5=\ln (276)/(680) \\ t=(6\ln (276)/(280))/(\ln 0.5) \\ t=7.8\text{ min} \end{gathered}`