Question

#7 determine if it involves independent or dependent and find the probability. how would you do this

Answer 1

Let's begin by listing out the given information:

Independence in probability means that the outcome of one event does not affect the outcome of the other event

Dependence means that the outcome of an event is tied to or affects the outcome of the other event

a)

white sock = 2

brown sock = 6

black sock = 6

Total sock = 14

I picked a first sock (white) & a second sock (brown)

Before picking the first sock, we have the probability to be:

`\begin{gathered} P(First)=\frac{NoOf\text{White}sock}{\text{Total}sock}=(2)/(14)=(1)/(7) \\ P(First)=(1)/(7) \end{gathered}`

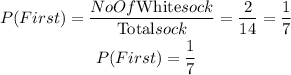
Because this is a probability without replacement, the number of socks left reduces by 1 to 13. It is from these 13 socks that we picked the second sock (brown) from.

After picking the first sock, we have the probability to be:

`\begin{gathered} P(Second)=\frac{NoOf\text{Brown}Sock}{\text{Total Sock Left}}=(6)/(14-1)=(6)/(13) \\ P(Second)=(6)/(13) \end{gathered}`

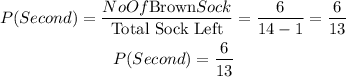
The probability in the first event is a different outcome from the second event. This shows dependence, hence, this is a dependent event

b)

This is a fair six-sided dice

Total outcome = 6

First roll (6) = 1

Second roll (5) = 1

The probability for the first roll is given by:

`P(FirstRoll)=\frac{\text{Number of sides with the number ''6'' }}{\text{Total Outcome}}=(1)/(6)`

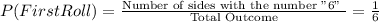
The probability for the second roll is given by:

`P(SecondRoll)=\frac{\text{Number of sides with the number ''5'' }}{\text{Total Outcome}}=(1)/(6)`

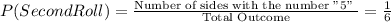
The probability in the first event is the same as the outcome of the second event. This shows independence, hence, this is an independent event

c)

A spinner has 3 regions. Each region has an equal chance of being landed upon

Total Outcome = 3

The probability for each spin is given by:

`\begin{gathered} P=\frac{\text{Possible Outcome}}{Total\text{ Outcome}}=(1)/(3) \\ P=(1)/(3) \end{gathered}`

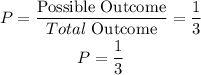
Each spin represents an independent outcome. Hence, this is an independent event

d)

A box contains 7 milk chocolates & 8 dark chocolates

Total (before picking) = 15 chocolates

Upon picking the first chocolate (milk), the probability is given as:

`\begin{gathered} P=\frac{\text{Number of Milk C}hocolates}{Total}=(7)/(15) \\ P=(7)/(15) \\ \end{gathered}`

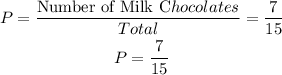
After the first pick, the total chocolates left is 14. You then randomly pick a dark chocolates, its probability is given as:

`\begin{gathered} P(2nd)=\frac{\text{Number Of Dark }chocolates}{Tota\text{l Left}}=(8)/(15-1)=(8)/(14)=(4)/(7) \\ P(2nd)=(4)/(7) \end{gathered}`

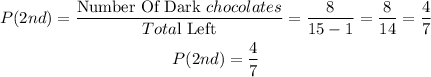
The probability in the first event is a different outcome from the second event. This shows dependence, hence, this is a dependent event