Initial:
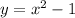
Changed to:
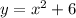
As you can see the change is: from -1 to +6.
In a equation as follow:
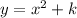
The k is a transformation that moves up or down the graph of the function. If k is changed to a less value the graph moves down, If k is changed to a greather number the graph moves up.
In this case the graph moves up
To find the number of units the graph moves find the difference betwwen values of k:
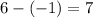
Then, the parabola y=x²-1 is moved 7 units up when it is changed to y=x²+6