Question

two verticals of a triangle are 8 in negative 5 And 8 and 7 if the area of the rectangles Is 72 square units named the possible location of the other 2 vertical

Answer 1

First let's find the length of the segment created by the two given points, using the formula:

`\begin{gathered} d=\sqrt[]{(y_2-y_1)^2+(x_2-x_1)^2} \\ d=\sqrt[]{(7-(-5))^2+(8-8)^2} \\ d=\sqrt[]{12^2} \\ d=12 \end{gathered}`

Since the given points have the same x-coordinate, we have a vertical segment, so the adjacents sides to this side will be horizontal segments.

In order to find the other vertices, first let's find the length of the horizontal sides, using the area formula:

`\begin{gathered} A=l\cdot w \\ 72=12\cdot w \\ w=(72)/(12)=6 \end{gathered}`

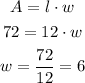
We can find the vertices by adding 6 to the x-coordinate of the given points, because then we will have the two horizontal sides of the rectangle:

`\begin{gathered} (8,-5)\to(8+6,-5)=(14,-5) \\ (8,7)\to(8+6,7)=(14,7) \end{gathered}`

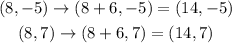
So the possible locations for the other 2 vertices are (14, -5) and (14, 7).