Question

Find the sum- 5 - 2 - 4/5 - 8/25

Answer 1

Given :

`-5,\text{ -2, -}(4)/(5),\text{ -}(8)/(25),\ldots`

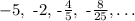
The sequence is a geometric progression. Recall that a G.P has a common ratio such that:

`\frac{Third\text{ term}}{Second\text{ term}}\text{ = }\frac{Second\text{ term}}{First\text{ term}}`

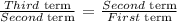
Let's go ahead to find the common ratio (r)

`\begin{gathered} (-(4)/(5))/(-2)\text{ = }(-(8)/(25))/(-(4)/(5))\text{ = }(2)/(5) \\ r\text{ = }(2)/(5) \end{gathered}`

To find the sum to infinity of geometric progression whose common ratio(r) is less than 1, we use the formula:

`S_(\infty)\text{ = }\frac{a}{1\text{ - r}}`

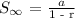
The first term (a) of the sequence = -5

Hence, the sum to infinity is:

`\begin{gathered} S_{\infty\text{ }}=\text{ }\frac{-5}{1\text{ - }(2)/(5)} \\ =\text{ -}(25)/(3) \end{gathered}`

Answer = -25/3