Question

The Choco-Latie Candies company makes candy-coated chocolates, 40% of which are red. The production line mixes the candies randomly and packages ten per box. Calculate the probability that at least 3 of the candies in a box are red. A: 0.8327B: 0.1693C: 0.2006D: 0.7624

Answer 1

From the problem, 40% are red and so 60% are not red.

The formula for calculating the probability of exact number of candies :

`P(r)=_nC_r(a)^r(b)^(n-r)`

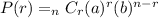
where n = number of sample

r = number of specific samples

a = percentage of one sample

b = percentage of the other sample

The problem is looking for the probability that at least 3 of the candies in a box are red.

This is also the same as the probability that at most 3 of the candies in a box are NOT red subtracted from 1.

`\begin{gathered} P(red)+P(notred)=1 \\ P(red)=1-P(notred) \end{gathered}`

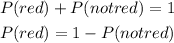
So we need to find the probability of having at most 3 candies are NOT red.

From the problem, n = 10 (because there are 10 candies in a box)

r = 0, 1 and 2 (these are the number of candies that are NOT red)

a = 40% or 0.4 (percentage of red candy)

b = 60% or 0.6 (percentage of not red candy)

The working equation will be :

`P(red\ge3)=1-\lbrack P(0)+P(1)+P(2)\rbrack`

So we need to find the probabilities of r = 0, 1 and 2.

For r = 0

`_(10)C_0(0.4)^0(0.6)^(10-0)=0.00605`

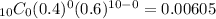
As you can see, the exponent of 0.4 is 0 because we need a candy that is NOT red. So it will be 0.

For r = 1

`_(10)C_1(0.4)^1(0.6)^(10-1)=0.04031`

For r = 2

`_(10)C_2(0.4)^2(0.6)^(10-2)=0.12093`

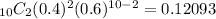
Using the working equation from above.

`\begin{gathered} P(red\ge3)=1-\lbrack0.00605+0.04031+0.12093\rbrack \\ =1-0.16729 \\ =0.83271 \end{gathered}`

The answer is A. 0.8327